RES: [gnso-wpm-dt] WPM: Preliminary Thoughts in Preparation for Step 6

["Jaime B Wagner" <j@xxxxxxxxxxxxxx>]

Please see my comments below

 

Jaime Wagner
j@xxxxxxxxxxxxxx

cel: (51)8126-0916

http://jaime-wagner.blogspot.com/

 

De: owner-gnso-wpm-dt@xxxxxxxxx [mailto:owner-gnso-wpm-dt@xxxxxxxxx] Em nome
de Gomes, Chuck
Enviada em: sexta-feira, 29 de janeiro de 2010 23:31
Para: Ken Bour; gnso-wpm-dt@xxxxxxxxx
Assunto: RE: [gnso-wpm-dt] WPM: Preliminary Thoughts in Preparation for Step
6

 

Thanks Ken.  Please see my comments below.

 

Chuck

 


  _____  


From: owner-gnso-wpm-dt@xxxxxxxxx [mailto:owner-gnso-wpm-dt@xxxxxxxxx] On
Behalf Of Ken Bour
Sent: Friday, January 29, 2010 7:18 PM
To: gnso-wpm-dt@xxxxxxxxx
Subject: [gnso-wpm-dt] WPM: Preliminary Thoughts in Preparation for Step 6

WPM Team Members:

 

In preparation for next Tuesday?s session (2 Feb 2010; 1700 UTC) in which we
are scheduled to discuss Step 6--Developing a Project Prioritization, I have
been thinking about this topic for several days and working through various
analyses of the model data generated thus far.  While I do not have specific
recommendations to offer the team, a few principles and questions are
beginning to take shape.  I thought I would share some of this thinking
ahead of time for those who have time to review and consider how the team
can apply what has been accomplished to date toward the ultimate objective.


 

NOTE:  I apologize in advance that this material is dense in places.  Please
do not attempt to digest it when you are stressed, preoccupied, and/or
multi-tasking which, I know, is the normal condition for ICANN volunteers
and Staff alike.  J 

 

As we discussed briefly on our call last Tuesday, the process of converting
from the two-dimensional matrix/chart to a one-dimensional prioritization is
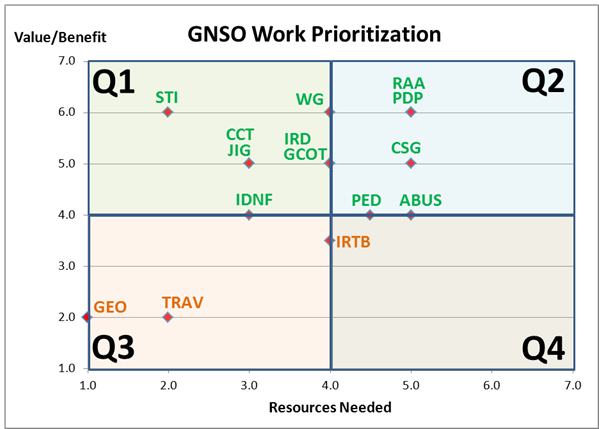
not necessarily straightforward.  To see why, let?s start with a current
picture of the DELPHI project placements on our 7-point scale chart.  

 



 

Accepting our definitions for X and Y and without making any unwarranted
assumptions, one set of interpretations from the four quadrants is as
follows (ignore the red dashed line for the moment):  

Q1 = High Value, Low Resources   à  Inarguably, these projects should have
the highest priority to commence or proceed.

Q4 = Low Value, High Resources   à  Similarly, these projects are obvious
candidates to be stopped, slowed down, or postponed.  [Note:  As can be
observed from the chart, the team?s test ratings did not produce any clear
Q4 cases.  At the risk of ?retrogressing? on a point (following Jaime?s
insightful lead), if high cross-correlation occurs between Resources Needed
and Value/Benefit, it is easy to predict that Q4 will be unpopulated.  If
that result can always be expected, it begs the question whether this model
is the correct one for a project prioritization task.  Normally, X and Y
must be INDEPENDENT variables in order to make a 4-Quadrant model work as
theoretically designed].  [Gomes, Chuck]  Note that IRTB is on the border of
Q4.  But even if it was in Q4, we are required to review the IRT Policy by
previous decisions made so I don't think we could eliminate it; at most all
we could do is slow it down, although in this case I think it has already
been slowed down. 

[Jaime] Although there is a correlation I don?t see it as necessary.  So I
think the X and Y as chosen are indeed independente. I just think that a
project requiring high resources with low relative value would not even
enter our prioritization list. After all, common sense still works without
the need for mathematical models.

Q2 = High Value, High Resources   à  On the surface (arithmetically), these
projects are no more important in terms of priority than those in Q3 as long
as the numerical scale (1-7) is essentially the same between Value and
Resources.  [Note:  if that conclusion is not immediately obvious, I will
shed more light on it further into this discussion].  [Gomes, Chuck]  I
don't follow you here at all.  It does may me start to question the
usefulness of this model though.  Could one of the problems be that we are
counting resources and value equivalently.  It seems to me that value is
more important than resources needed except in cases where resources needed
exceed resources available.  So maybe we need to add a step in the process
that estimates availability of resources; if that was doable, then we could
focus mainly on the value/benefit. Another way to approach it would be to
rank value/benefit and then assign resources in order from highest value to
lowest up to whatever limits we have.

[Jaime] Entirely agree with Chuck. I don?t agree with your affirmation that
Q2 and Q3 are equivalent. Value counts much more than resources needed. Only
when values are equivalent resources needed should be favored. But a low use
of resources says nothing about a project?s importance.

Q3 = Low Value, Low Resources   à  (the converse of Q2)

 

We are left, then, with two quadrants that produce relatively clear
action-strategies and two buckets in which the results are ambiguous.  How
might we resolve the Q2/Q3 issue?  

[Jaime] Again: I don?t see a problem here. And Ken, sorry, but I feel the
next paragraphs are a tempest in a glass of water: an intricate solution for
a no-problem.

In my view, value (Y axis) is our main concern. Priority ?is? importance or
value. Only when we have similar value projects, resources needed (X) should
be considered to produce a straight list.

 

One straightforward approach is to take the rating results for Value/Benefit
and multiply them by Resources Needed and then sort by those products.  A
project that is rated 7 on Value/Benefit and 7 on Resources Needed (i.e. not
needed) is the maximum result (7 * 7 = 49) we could achieve with this
scaling.  First, we must recognize that ?Far Below Average? Resources Needed
is a positive result, but we assigned it the value of 1 (lowest on the
scale) for convenience.  In order to make the math work properly, we have to
reverse all of the X values by subtracting them from 8.  So, TRAV is rated
Y=2, X=2 on the chart, but Resources Needed would actually count as a 6 if
we had reversed the scale when rating originally.  To save everyone the
arithmetic exercise, the table below shows the conversions.  

 


X Scale

Far Below

Moderately Below

Slightly Below

Average

Slightly Above

Moderately Above

Far Above


Original

1

2

3

4

5

6

7


Reversed

7

6

5

4

3

2

1

 

If we take all of the project DELPHI scores for Y and X (converted) and
multiply them together we get the following ranking:

 


Project

Resources

Value

R-Converted

(R-C)*V

Rank


STI

2.0

6.0

6.0

36.0

1


JIG

3.0

5.0

5.0

25.0

2


CCT

3.0

5.0

5.0

25.0

2


WG

4.0

6.0

4.0

24.0

4


GCOT

4.0

5.0

4.0

20.0

5


IRD

4.0

5.0

4.0

20.0

5


IDNF

3.0

4.0

5.0

20.0

5


PDP

5.0

6.0

3.0

18.0

8


RAA

5.0

6.0

3.0

18.0

8


CSG

5.0

5.0

3.0

15.0

10


PED

4.5

4.0

3.5

14.0

11


GEO

1.0

2.0

7.0

14.0

11


IRTB

4.0

3.5

4.0

14.0

11


ABUS

5.0

4.0

3.0

12.0

14


TRAV

2.0

2.0

6.0

12.0

14

 

Note:  The column labeled ?R-Converted? contains the adjusted X values by
taking each original score and subtracting it from 8. 

 

Toward the bottom of the list (Rank=11), notice that PED, GEO, and IRTB all
have the same score (14.0) even though they occupy very different spatial
locations on the chart (Q2 and Q3).  Similarly, ABUS and TRAV (Rank=14) have
the same result while being in opposite quadrants.  As mentioned earlier in
the narrative, this apparent anomaly occurs because of the scale equality
between Value/Benefit and Resources Needed. [Gomes, Chuck]  As mentioned
above, I think this may be a problem.  Since the same 1-7 point scale is
used for both dimensions (equally weighted), a 2 on Value/Benefit has the
same effect as a 2 on Resources Needed (after conversion).  Given a single
rating scale for both dimensions, theoretically, we should be ambivalent in
choosing between a project that is Far Above Average on Value/Benefit
(Rating=7) and one that is Far Below Average on Resources Needed (Converted
Rating=7).  On the other hand, some team members may perceive that a project
with HIGH Value/Benefit is more important than one having comparably LOW
Resources Needed and, thus, would give a higher priority to PED and ABUS
even though GEO is actually tied with PED and scores higher than ABUS!   I
will take up that question a bit further into the analysis? 

 

How might we remedy this ambivalence between Q2/Q3?  

 

One way to resolve this problem is to consider a straight line that starts
at 1,1 and goes to 7,7 (see red dashed line in above chart).  Any project
whose Value/Benefit is >= Resources Needed is considered in the ACCEPT area
and any project whose Value is < Resources is in the QUESTIONABLE region.
One interpretation is that projects in the QUESTIONABLE region, relatively
speaking, are consuming more resources than the value they are generating
and are candidates for being reevaluated.  In terms of relative priority,
those points furthest from the red line are the least important projects.
[Gomes, Chuck]  Do you mean furthest below the red line?  ABUS would be the
lowest ranked project using this approach.  [Gomes, Chuck]  I think this
idea may be promising but there are some anomolies.  Note: the IRTB is below
the line but it is a required task; FF is above the line and may be one of
the least important tasks because at best it could produce some best
practices. Should PDPs have more value than non-PDPs?  I don't know but
maybe. 

 

Another possibility is to develop a weighting system for Value/Benefit that
is different from Resources Needed, that is, alter the scales to accord
more/less weight to Y than X.  Incidentally, although it may seem to be an
obvious solution, multiplying either series by a constant number (e.g. 4 for
Y and 2 for X) will produce identical project rankings.  Said another way,
the X/Y dimension weights cannot be simple multiples of each other.  To
illustrate an approach that would produce a unique ranking, suppose (see
table below) we decided to use a Fibonacci series (remember the SCRUM
discussion back in mid-December?) for the Y weights (starting arbitrarily at
2) and a straight linear weighting for X matching the original scale.  

 


Y-Scale

Y-Weight

X-Scale

X-Weight


1

2

1

1


2

3

2

2


3

5

3

3


4

8

4

4


5

13

5

5


6

21

6

6


7

34

7

7

 

If we multiply these series together, it produces a prioritization shown in
the table below.  The column labeled ?V*C?[Gomes, Chuck]  Do you mean "V*R"?
contains the product of the weighted results.  

 


Project

Resources

Value

R-Converted

V-Wgt

R-Wgt

V*R

Rank


STI

2.0

6.0

6.0

21.0

6.0

126.0

1


WG

4.0

6.0

4.0

21.0

4.0

84.0

2


JIG

3.0

5.0

5.0

13.0

5.0

65.0

3


CCT

3.0

5.0

5.0

13.0

5.0

65.0

3


PDP

5.0

6.0

3.0

21.0

3.0

63.0

5


RAA

5.0

6.0

3.0

21.0

3.0

63.0

5


GCOT

4.0

5.0

4.0

13.0

4.0

52.0

7


IRD

4.0

5.0

4.0

13.0

4.0

52.0

7


IDNF

3.0

4.0

5.0

8.0

5.0

40.0

9


CSG

5.0

5.0

3.0

13.0

3.0

39.0

10


PED

4.5

4.0

3.5

8.0

3.0

24.0

11


ABUS

5.0

4.0

3.0

8.0

3.0

24.0

11


GEO

1.0

2.0

7.0

3.0

7.0

21.0

13


IRTB

4.0

3.5

4.0

5.0

4.0

20.0

14


TRAV

2.0

2.0

6.0

3.0

6.0

18.0

15

 

Using this method, TRAV is the lowest ranked project followed by IRTB, GEO,
and ABUS.  

 

There are myriad possibilities for weightings that could be applied to X and
Y differently, but I will stop here since the first step would be to develop
a rationale for such treatment.  Once a justification is produced as to why
Y should be weighted higher than X (or vice versa),[Gomes, Chuck]  I think
this could be justified as noted above.  it is much easier to create a
numbering scheme that supports it. 

 

Another option, as suggested on last week?s call, is to create a new
prioritization/ranking using the above information as INPUT.  One could
start by ranking projects within quadrants, for example, Q1, then Q2/Q3
(challenging?!), and, finally Q4.  If this is a viable option, a reasonable
question that might be asked is:  Is it possible to rank all of the projects
from 1 to 15 (or n) without first exercising the X/Y modeling step?  If the
answer is YES, then this entire process could be radically abridged.  If NO,
then the X/Y modeling is a useful precursor to developing rankings within
quadrants.  [Note:  a process needs to be developed for generating the
individual quadrant rankings, e.g. group Delphi?]  [Gomes, Chuck] I am not
convinced we need to rank quadrants linearly.  It might suffice to rank them
in groups. 

 

At this stage, Staff is neither leaning toward nor recommending any
particular solution, only exploring options and posing questions that the
team may want to consider in its ensuing deliberations.  

 

Additional questions that might be productive to discuss as Step 6 unfolds:


 

·         In what specific ways will a prioritized list of projects assist
the Council?  

·         Should the prioritization result in an unambiguous ranking from 1
to n (no ties) or can projects be grouped into one or more buckets? [Gomes,
Chuck]  I favor this as I said above.  

·         What decisions or outcomes does the team expect from executing the
rating/ranking/prioritization processes?  

·         How are new projects added to the list and incorporated into the
process in terms of evaluation/ranking? 

·         Since the rating process is relative, is it possible to slot a new
project into the matrix/chart without reevaluating all of the others at the
same time?

·         How are changes to project status identified, recommended,
approved, and incorporated?  

·         What frequency should the WPM process be exercised (e.g. monthly,
semi-annually, annually) or, if ad hoc, what trigger events cause one to be
initiated? 

 

Again, I apologize for the length and complexity of this email, but I
thought it might be helpful to document some of my ruminations prior to our
next session.  

 

Regards,

 

Ken Bour