RE: [gnso-wpm-dt] WPM: Preliminary Thoughts in Preparation for Step 6

["Gomes, Chuck" <cgomes@xxxxxxxxxxxx>]

Thanks Ken.  Please see my comments below.
 
Chuck


________________________________

        From: owner-gnso-wpm-dt@xxxxxxxxx [mailto:owner-gnso-wpm-dt@xxxxxxxxx] 
On Behalf Of Ken Bour
        Sent: Friday, January 29, 2010 7:18 PM
        To: gnso-wpm-dt@xxxxxxxxx
        Subject: [gnso-wpm-dt] WPM: Preliminary Thoughts in Preparation for 
Step 6
        
        

        WPM Team Members:

         

        In preparation for next Tuesday's session (2 Feb 2010; 1700 UTC) in 
which we are scheduled to discuss Step 6--Developing a Project Prioritization, 
I have been thinking about this topic for several days and working through 
various analyses of the model data generated thus far.  While I do not have 
specific recommendations to offer the team, a few principles and questions are 
beginning to take shape.  I thought I would share some of this thinking ahead 
of time for those who have time to review and consider how the team can apply 
what has been accomplished to date toward the ultimate objective.  

         

        NOTE:  I apologize in advance that this material is dense in places.  
Please do not attempt to digest it when you are stressed, preoccupied, and/or 
multi-tasking which, I know, is the normal condition for ICANN volunteers and 
Staff alike.  J 

         

        As we discussed briefly on our call last Tuesday, the process of 
converting from the two-dimensional matrix/chart to a one-dimensional 
prioritization is not necessarily straightforward.  To see why, let's start 
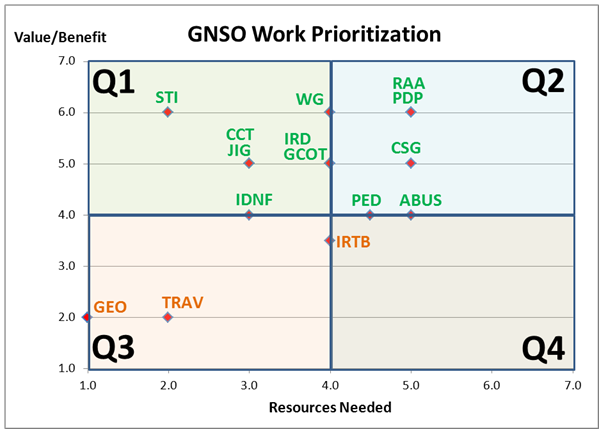
with a current picture of the DELPHI project placements on our 7-point scale 
chart.  

         

          

         

        Accepting our definitions for X and Y and without making any 
unwarranted assumptions, one set of interpretations from the four quadrants is 
as follows (ignore the red dashed line for the moment):  

        Q1 = High Value, Low Resources   à  Inarguably, these projects should 
have the highest priority to commence or proceed.

        Q4 = Low Value, High Resources   à  Similarly, these projects are 
obvious candidates to be stopped, slowed down, or postponed.  [Note:  As can be 
observed from the chart, the team's test ratings did not produce any clear Q4 
cases.  At the risk of "retrogressing" on a point (following Jaime's insightful 
lead), if high cross-correlation occurs between Resources Needed and 
Value/Benefit, it is easy to predict that Q4 will be unpopulated.  If that 
result can always be expected, it begs the question whether this model is the 
correct one for a project prioritization task.  Normally, X and Y must be 
INDEPENDENT variables in order to make a 4-Quadrant model work as theoretically 
designed].  [Gomes, Chuck]  Note that IRTB is on the border of Q4.  But even if 
it was in Q4, we are required to review the IRT Policy by previous decisions 
made so I don't think we could eliminate it; at most all we could do is slow it 
down, although in this case I think it has already been slowed down. 

        Q2 = High Value, High Resources   à  On the surface (arithmetically), 
these projects are no more important in terms of priority than those in Q3 as 
long as the numerical scale (1-7) is essentially the same between Value and 
Resources.  [Note:  if that conclusion is not immediately obvious, I will shed 
more light on it further into this discussion].  [Gomes, Chuck]  I don't follow 
you here at all.  It does may me start to question the usefulness of this model 
though.  Could one of the problems be that we are counting resources and value 
equivalently.  It seems to me that value is more important than resources 
needed except in cases where resources needed exceed resources available.  So 
maybe we need to add a step in the process that estimates availability of 
resources; if that was doable, then we could focus mainly on the value/benefit. 
Another way to approach it would be to rank value/benefit and then assign 
resources in order from highest value to lowest up to whatever limits we have. 

        Q3 = Low Value, Low Resources   à  (the converse of Q2)

         

        We are left, then, with two quadrants that produce relatively clear 
action-strategies and two buckets in which the results are ambiguous.  How 
might we resolve the Q2/Q3 issue?  

         

        One straightforward approach is to take the rating results for 
Value/Benefit and multiply them by Resources Needed and then sort by those 
products.  A project that is rated 7 on Value/Benefit and 7 on Resources Needed 
(i.e. not needed) is the maximum result (7 * 7 = 49) we could achieve with this 
scaling.  First, we must recognize that "Far Below Average" Resources Needed is 
a positive result, but we assigned it the value of 1 (lowest on the scale) for 
convenience.  In order to make the math work properly, we have to reverse all 
of the X values by subtracting them from 8.  So, TRAV is rated Y=2, X=2 on the 
chart, but Resources Needed would actually count as a 6 if we had reversed the 
scale when rating originally.  To save everyone the arithmetic exercise, the 
table below shows the conversions.  

         

X Scale

Far Below

Moderately Below

Slightly Below

Average

Slightly Above

Moderately Above

Far Above

Original

1

2

3

4

5

6

7

Reversed

7

6

5

4

3

2

1

         

        If we take all of the project DELPHI scores for Y and X (converted) and 
multiply them together we get the following ranking:

         

Project

Resources

Value

R-Converted

(R-C)*V

Rank

STI

2.0

6.0

6.0

36.0

1

JIG

3.0

5.0

5.0

25.0

2

CCT

3.0

5.0

5.0

25.0

2

WG

4.0

6.0

4.0

24.0

4

GCOT

4.0

5.0

4.0

20.0

5

IRD

4.0

5.0

4.0

20.0

5

IDNF

3.0

4.0

5.0

20.0

5

PDP

5.0

6.0

3.0

18.0

8

RAA

5.0

6.0

3.0

18.0

8

CSG

5.0

5.0

3.0

15.0

10

PED

4.5

4.0

3.5

14.0

11

GEO

1.0

2.0

7.0

14.0

11

IRTB

4.0

3.5

4.0

14.0

11

ABUS

5.0

4.0

3.0

12.0

14

TRAV

2.0

2.0

6.0

12.0

14

         

        Note:  The column labeled "R-Converted" contains the adjusted X values 
by taking each original score and subtracting it from 8. 

         

        Toward the bottom of the list (Rank=11), notice that PED, GEO, and IRTB 
all have the same score (14.0) even though they occupy very different spatial 
locations on the chart (Q2 and Q3).  Similarly, ABUS and TRAV (Rank=14) have 
the same result while being in opposite quadrants.  As mentioned earlier in the 
narrative, this apparent anomaly occurs because of the scale equality between 
Value/Benefit and Resources Needed. [Gomes, Chuck]  As mentioned above, I think 
this may be a problem.  Since the same 1-7 point scale is used for both 
dimensions (equally weighted), a 2 on Value/Benefit has the same effect as a 2 
on Resources Needed (after conversion).  Given a single rating scale for both 
dimensions, theoretically, we should be ambivalent in choosing between a 
project that is Far Above Average on Value/Benefit (Rating=7) and one that is 
Far Below Average on Resources Needed (Converted Rating=7).  On the other hand, 
some team members may perceive that a project with HIGH Value/Benefit is more 
important than one having comparably LOW Resources Needed and, thus, would give 
a higher priority to PED and ABUS even though GEO is actually tied with PED and 
scores higher than ABUS!   I will take up that question a bit further into the 
analysis... 

         

        How might we remedy this ambivalence between Q2/Q3?  

         

        One way to resolve this problem is to consider a straight line that 
starts at 1,1 and goes to 7,7 (see red dashed line in above chart).  Any 
project whose Value/Benefit is >= Resources Needed is considered in the ACCEPT 
area and any project whose Value is < Resources is in the QUESTIONABLE region.  
One interpretation is that projects in the QUESTIONABLE region, relatively 
speaking, are consuming more resources than the value they are generating and 
are candidates for being reevaluated.  In terms of relative priority, those 
points furthest from the red line are the least important projects. [Gomes, 
Chuck]  Do you mean furthest below the red line?  ABUS would be the lowest 
ranked project using this approach.  [Gomes, Chuck]  I think this idea may be 
promising but there are some anomolies.  Note: the IRTB is below the line but 
it is a required task; FF is above the line and may be one of the least 
important tasks because at best it could produce some best practices. Should 
PDPs have more value than non-PDPs?  I don't know but maybe. 

         

        Another possibility is to develop a weighting system for Value/Benefit 
that is different from Resources Needed, that is, alter the scales to accord 
more/less weight to Y than X.  Incidentally, although it may seem to be an 
obvious solution, multiplying either series by a constant number (e.g. 4 for Y 
and 2 for X) will produce identical project rankings.  Said another way, the 
X/Y dimension weights cannot be simple multiples of each other.  To illustrate 
an approach that would produce a unique ranking, suppose (see table below) we 
decided to use a Fibonacci series (remember the SCRUM discussion back in 
mid-December?) for the Y weights (starting arbitrarily at 2) and a straight 
linear weighting for X matching the original scale.  

         

Y-Scale

Y-Weight

X-Scale

X-Weight

1

2

1

1

2

3

2

2

3

5

3

3

4

8

4

4

5

13

5

5

6

21

6

6

7

34

7

7

         

        If we multiply these series together, it produces a prioritization 
shown in the table below.  The column labeled "V*C"[Gomes, Chuck]  Do you mean 
"V*R"?  contains the product of the weighted results.  

         

Project

Resources

Value

R-Converted

V-Wgt

R-Wgt

V*R

Rank

STI

2.0

6.0

6.0

21.0

6.0

126.0

1

WG

4.0

6.0

4.0

21.0

4.0

84.0

2

JIG

3.0

5.0

5.0

13.0

5.0

65.0

3

CCT

3.0

5.0

5.0

13.0

5.0

65.0

3

PDP

5.0

6.0

3.0

21.0

3.0

63.0

5

RAA

5.0

6.0

3.0

21.0

3.0

63.0

5

GCOT

4.0

5.0

4.0

13.0

4.0

52.0

7

IRD

4.0

5.0

4.0

13.0

4.0

52.0

7

IDNF

3.0

4.0

5.0

8.0

5.0

40.0

9

CSG

5.0

5.0

3.0

13.0

3.0

39.0

10

PED

4.5

4.0

3.5

8.0

3.0

24.0

11

ABUS

5.0

4.0

3.0

8.0

3.0

24.0

11

GEO

1.0

2.0

7.0

3.0

7.0

21.0

13

IRTB

4.0

3.5

4.0

5.0

4.0

20.0

14

TRAV

2.0

2.0

6.0

3.0

6.0

18.0

15

         

        Using this method, TRAV is the lowest ranked project followed by IRTB, 
GEO, and ABUS.  

         

        There are myriad possibilities for weightings that could be applied to 
X and Y differently, but I will stop here since the first step would be to 
develop a rationale for such treatment.  Once a justification is produced as to 
why Y should be weighted higher than X (or vice versa),[Gomes, Chuck]  I think 
this could be justified as noted above.  it is much easier to create a 
numbering scheme that supports it. 

         

        Another option, as suggested on last week's call, is to create a new 
prioritization/ranking using the above information as INPUT.  One could start 
by ranking projects within quadrants, for example, Q1, then Q2/Q3 
(challenging?!), and, finally Q4.  If this is a viable option, a reasonable 
question that might be asked is:  Is it possible to rank all of the projects 
from 1 to 15 (or n) without first exercising the X/Y modeling step?  If the 
answer is YES, then this entire process could be radically abridged.  If NO, 
then the X/Y modeling is a useful precursor to developing rankings within 
quadrants.  [Note:  a process needs to be developed for generating the 
individual quadrant rankings, e.g. group Delphi?]  [Gomes, Chuck] I am not 
convinced we need to rank quadrants linearly.  It might suffice to rank them in 
groups. 

         

        At this stage, Staff is neither leaning toward nor recommending any 
particular solution, only exploring options and posing questions that the team 
may want to consider in its ensuing deliberations.  

         

        Additional questions that might be productive to discuss as Step 6 
unfolds:  

         

        ·         In what specific ways will a prioritized list of projects 
assist the Council?  

        ·         Should the prioritization result in an unambiguous ranking 
from 1 to n (no ties) or can projects be grouped into one or more buckets? 
[Gomes, Chuck]  I favor this as I said above.  

        ·         What decisions or outcomes does the team expect from 
executing the rating/ranking/prioritization processes?  

        ·         How are new projects added to the list and incorporated into 
the process in terms of evaluation/ranking? 

        ·         Since the rating process is relative, is it possible to slot 
a new project into the matrix/chart without reevaluating all of the others at 
the same time?

        ·         How are changes to project status identified, recommended, 
approved, and incorporated?  

        ·         What frequency should the WPM process be exercised (e.g. 
monthly, semi-annually, annually) or, if ad hoc, what trigger events cause one 
to be initiated? 

         

        Again, I apologize for the length and complexity of this email, but I 
thought it might be helpful to document some of my ruminations prior to our 
next session.  

         

        Regards,

         

        Ken Bour